KNN (K Near Neighborhood)

## Ⅰ. 측위기반의 KNN(K-Nearest Neighbor) 알고리즘의 개요 ### 가. KNN 알고리즘의 정의 - 새로운 fingerprint를 기존 클러스터 내의 모든 데이터와 Instance 기반거리를 측정하여 가장 많은 속성을 가진 클러스터에 할당하는 군집알고리즘 - Sample 에 주어진 x(샘플)에서 가장 가까운 k개의 원소가 많이 속하는 class로 x를 분류하는 비모수적 확률밀도 추정방법 ### 나. KNN 알고리즘의 특징 | 특징 | 설명 | | -------- | -------- | | **최고인접 다수결** | 기존 데이터중 가장 유사한 k개의 데이터를 측정하여 분류 | | **유사도(거리) 기반** | 유클리디안 거리(Euclidian's distance), 마할라노비스의 거리(Mahalanobis' distance), 코사인 유사도(cosine similarity)등을 활용 | | **Lazy learning 기법** | 새로운 입력 값이 들어온 후 분류시작| | **단순유연성** | 모형이 단순하며 파라미터의 가정이 거의 없음 | | **NN(Nearest Neighbors)개선** | - **KNN**은 **가장 근접한 k개의 데이터에 대한 다수결 내지 가중합계 방식**으로 분류
- **NN의 경우** 새로운 항목을 분류할 때 가장 유사한 instance를 찾아서 같은 class에 일방적으로 분류 시 **잡음 섞인 데이터에는 성능이 좋지 못함** | ### 다. 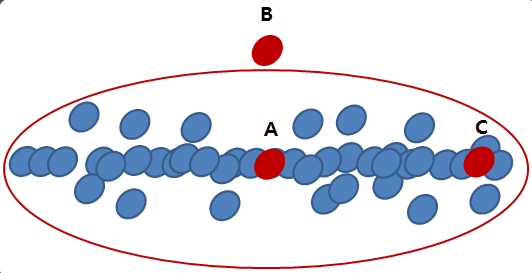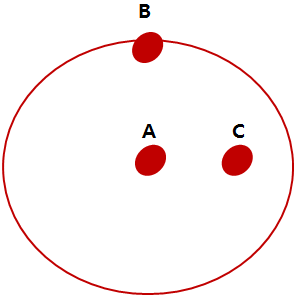KNN 알고리즘에 대한 거리의 개념 - **유클리디안 거리(Euclidian's distance)**: 점과 전간의 최단 거리 - **마할라노비스의 거리(Mahalanobis' distance)**: 두 모집단들을 판별하는 문제에서 두 집단 사이의 거리(확률분포를 고려한 거리- 이때 화이트닝 변환(whitening transform)을 사용) - **코사인 유사도(cosine similarity)**: 내적 공간의 두 벡터간 각도의 코사인값을 이용하여 측정된 벡터간의 유사한 정도 | 이미지 1 | 이미지 2 | | -------- | -------- | |  | | - 유클리디안 거리는 A와 B가 가장 가까움 - 마할라노비스의 거리는 A와 C가 가장 가까움(확률분포를 고려) 확률 분포를 고려하기 위해 화이트닝 변환을 하며 오른쪽에 A,B,C만 있는 그림이 변환후 모습임 - **이외 KNN에 사용되는 유사도 측정방법: 상관계수, 마니모토점수 등** ## Ⅱ. KNN 알고리즘의 동작원리 ### 가. 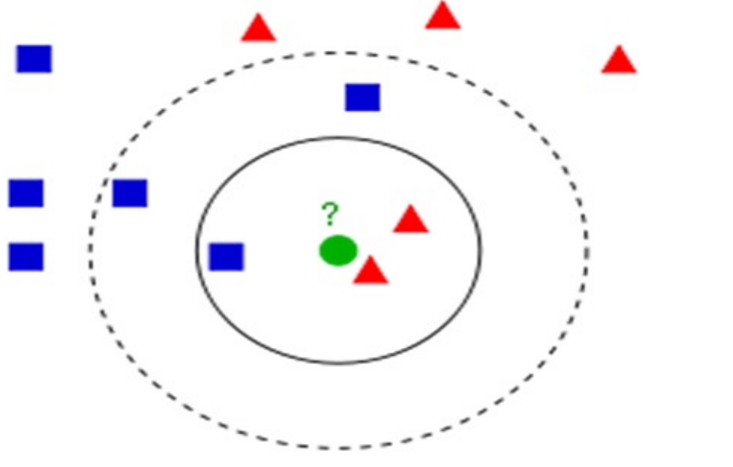K값 결정과 분류의 원리 - 새로운 fingerprint(원)을 네모 또는 삼각형의 클러스터에 매칭원리  1) 새로운 fingerprint입력(물음표, 동그라미) 확인
2) 거리기반 k개 데이터를 training set에서 추출
3) 추출데이터들의 클러스터, label 확인
4) 다수결(Majority voting) 의한 클러스터 매칭
- **결과 새로운 fingerprint는 K가 3인 경우 삼각형, 5인 경우 사각형 클러스터에 매칭됨** ### 나. KNN 알고리즘의 상세 동작원리 | 동작원리 | 설명 | | -------- | -------- | | **fingerprint확인** | - 새로운 입력값 확인
- 가까운 데이터는 같은 **Label(클러스터 가능성 큼)**
- 기존의 모든 데이터와 새로운 ingerprint와 비교준비 | | **명목변수기반 그룹분류**| - 기존의 저장되어있는 데이터 셋의 label화
- 서로 다른 범주 데이터를 정규화 수행
- 분류기 검사 수행
예: 데이터의 90%를 훈련데이터 10%를 테스트로 활용 | | **거리측정** | - 유클리디언 거리
- 메모리기반 fingerprint와 모든 데이터간의 거리계산
- 계산된 거리의 정렬수행 | | **K 선정** | - 양의 정수값, 정렬된 거리중 가장 가까운 k개 데이터 선정
- 여러 k값을 모델링 후 가장 성능이 좋은 k값 선정
- 노이즈 클수록 큰 k값 선정이 좋음
- 작은 k는 극단값 및 노이즈를 허용하여 클러스터링 오류가능| | **클러스터 매칭** | - 명목 데이터 경우, 다수결(majority voting)기반의 클러스터 매칭 수행, k개 데이터가 많이 속해있는 클러스터로 새로운 값을 분류
- 수치형 데이터의 경우 k개 데이터의 평균(or 가중평균)을 이용하여 클러스터 매칭 | ## Ⅲ. KNN 알고리즘의 장단점 ### 가. 장점 | 장점 | 설명 | | -------- | -------- | | **효율성** | 훈련데이터에 잡음이 있는 경우에도 적용가능 | | **결과일관성** | - 훈련데이터의 크기가 클 경우 효율적임
(데이터의 수가 무한대로 증가 시 오차율이 베이즈 오차율의 두배보다 항상 나쁘지 않음을 보장)
- 임의의 k값에 대해 베이즈 오차율에 항상 근접함을 보장 | | **학습간단** | - 모형이 단순하고 쉬운 구현 가능 | | **유연한 경계** | - 거리의 변형, 가중치 적용용이
- 유클리디언,코사인유사도, 가중치 적용, 정규화적용 용이 | | **모델의 유연성** | - 데이터에 대한 가정 반영 및 변형이 간편
- 변형데이터의 training data set 기반 분류기 검증용이 | | **높은 정확도** | - 사례기반으로 높은 정확성
- 훈련데이터 클수록 클러스터 매칭 정확성 좋아짐 | ### 나. 단점 | 단점 | 설명 | | -------- | -------- | | **성능 가변성** | - k값 선정에 따라 알고리즘의 성능이 좌우됨
- k값 최적화, under/overfitting의 고려필요 | | **높은 자원요구량** | - 데이터 셋 전체를 읽어서 메모리에 기억
- 새로운 개체 n을 읽어서 메모리 내의 데이터 셋과 비교 | | **고비용** | - 모든 훈련샘플과의 거리를 계산하여야 하므로 연산비용(cost)이 높음 | | **공간예측 부정확** | - 공간정보 예측모델에서는 영향변수 많이 적용이 어려움 | | **거리계산 복잡성** | - 모든 데이터와의 유사도, 거리측정 수행필요 | | **노이즈에 약함** | - 노이즈로 인해 큰 k 설정을 필요로 함
- 민감하고 작은 데이터 무시되는 under fitting 문제야기 | ## Ⅳ. KNN 알고리즘의 활용방안 | 활용방안 | 설명 | 사례 | | -------- | -------- | -------- | | **위치측위**|이동객체의 위치에서 AP 신호강도를 측정하고 이를 KNN 알고리즘을 활용하여 이동객체의 위치를 최종적으로 추정|**MS사의 RADAR - Ekahau Inc의 Wi-Fi RLS, COMPAS**| | **선호도 분류** | 사용자의 추천정보 기반 성향/구매패턴분류 |**내용기반 추천 시스템** | | **데이터필터링** |포털등의 중복, 유사 게시글 필터링 | **문서분류(빈발항목집합, 빈발단어집합 등**) | | **고속도로 통행시간 예측** | TCS 교통량 및 DSRC 구간 통행시간의 실시간 자료를 KNN 기반으로 분석 |**차량 근거리 무선통신(DSRC) 활용 통행시간 예측**|