Cross Validation
태그 :
- 개념
- Training Set, Validation Set, Test Set, Random subsampling, k-fold cross validation 교차 검증 (Cross Validation)의 정의 Data Set을 K개의 training Set 또는 부분집합과 나머지 Test Set으로 구분, Training Set을 이용하여 학습하고, 나머지 Test Set으로 성능 측정한 데이터를 얻어, 이에 대한 평균을 구하여 모델 성능을 평가하는 기법
## Ⅰ. 적은 샘플을 이용한 Machine learning 모델 타당성 평가 기법, 교차 검증의 개요
### 가. Machine Learning 중 지도학습(Supervised learning) 모델의 검증 현안
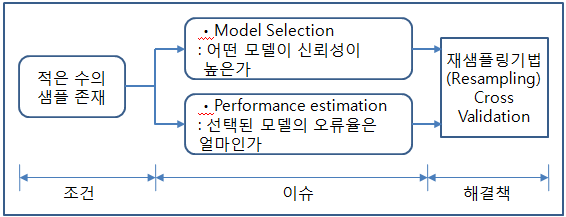
1) 데이터Set의 질적, 양적 품질은 데이터 모델의 성능을 좌우함
2) 데이터의 수집에 많은 비용 문제로 대부분 데이터의 양이 부족한 현실에서, 재 샘플링 기법을 사용하면 성능 측정의 신뢰도를 높일 수 있음.
3) 대표적인 재 샘플링 기법으로 Cross-Validation, Bootstrap 기법이 있음
### 나. 교차 검증 (Cross Validation)의 정의 - Data Set을 K개의 training Set 또는 부분집합과 나머지 Test Set으로 구분, Training Set을 이용하여 학습하고, 나머지 Test Set으로 성능 측정한 데이터를 얻어,
이에 대한 평균을 구하여 모델 성능을 평가하는 기법 ### 다. Data Set의 구분 |데이터 Set | 설명 | 활용 |
| -------- | -------- | -------- |
| Training Set | 모형을 적합화시키기 위해 사용되는 데이터 | 모델 학습 |
| Test Set | 최종 선택모형이 새로운 데이터에 대하여 좋은 성과를 갖는지 평가 | 모델 평가 |
| Validation Set | 모형이 얼마나 잘 적합화 되었는지 평가
일부 모형을 조정하여 구축된 모형 중 좋은 모형 선택 | 모델 선택 | ## Ⅱ. 교차 검증 (Cross Validation) 방법 ### 가. Random Subsampling - S를 랜덤하게 k개의 training set과 test set으로 나눔. S_train은 약 70%로 구성하며, 모델 학습용으로 쓰고 나머지 S_cv는 평가용으로 사용. - 각 모델 M_i를 S_train 으로 학습시켜 hypothesis h_i를 구함 - S_cv(h_i)를 적용하였을 때 error(generation error)를 최소화하는 모델선택 - 옵션으로 모델을 선택 후 그 모델에 S_cv도 학습 - 이 방식의 단점은 빼 놓은 30%는 데이터를 학습-평가에 반영하지 않음 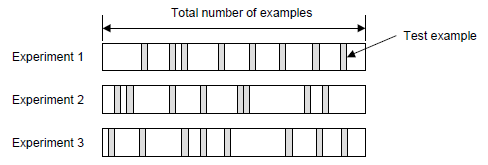 - 에러율 : 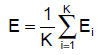 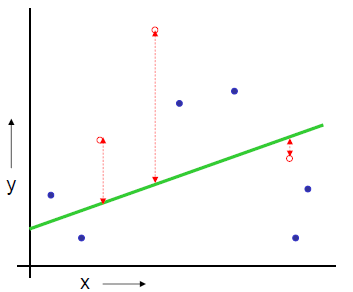 ### 나. k-fold cross validation - Training Set S을 k개의 부분 집합으로 등분, k-1개로 학습하고 나머지 한 개로 테스트. - 각 모델 M_i에 대해 J번째 (j=1,..,k) 집합 S_j를 제외시키고 학습시켜 h_ij를 구하고, S_j를적용하여 generation error 들을 구함 - 모델 M_i의 에러는 각 j번째의 에러들의 평균으로 함. (가장 작은 에러를 갖는 모델 선택) - 그후, 전체 데이터 S로 학습 - 이 방식의 단점은 전형적인 k값은 10이지만, 항상 적정하지는 않고, k값에 따라 계산량이많아짐  - 에러율 : 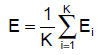 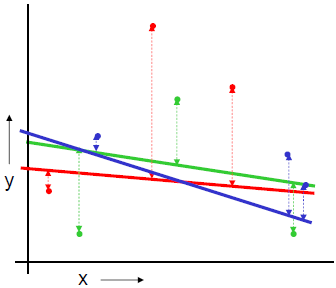 ### 다. Leave-one-out cross validation - k fold cross validation에서, k=N인 경우(N은 샘플 개수) 하나 남기기(Leave-one-out) 또는 잭나이프(Jackknife) 기법 이라 함 - 결국, 데이터 1개씩을 빼가면서 모든 테스트를 하는 방법.  - 에러율 : 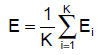 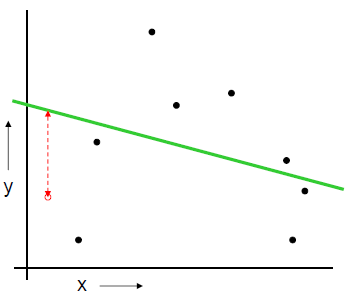 < 1회 > 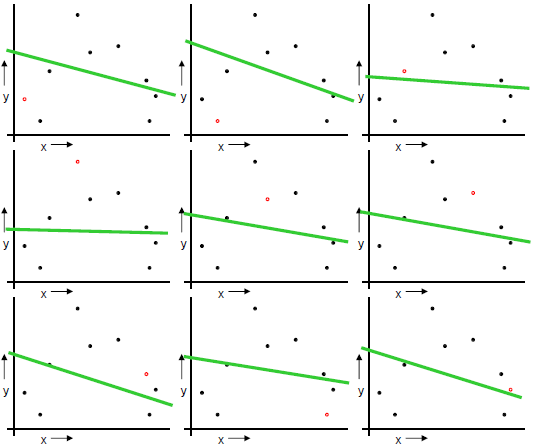 < N 회 반복 > ## Ⅲ. 검증 방법의 비교 |항목 | Train-validation | Cross-Validation |Bootstrap |
| -------- | -------- | -------- |-------- |
| **개념** | 훈련집합, 테스트 집합, 검증
집합을 통해서 모델의
정확도를 검증 | 데이터를 k개의 집합으로 나누어
검증한 결과의 평균치로 모델
검증 | 전체 데이터에서 무작위 복원
추출로 훈련집합 생성 하여
검증하는 방법 | | **활용기준** | 데이터가 충분히 많은 경우 | 데이터가 충분하지 않은 경우 |데이터가 충분하지 않은 경우,
모집단 분포 가정 어려운 경우| | **데이터 set** | Train Set, Test Set,
Validation Set | K개의 Set 분류(k-fold)
k-1 : Train set
1 : Test set | N개의 Bootstrap sample | | **정확도** | 에러율 예측의 정확도 다소
**정확도** 낮음 | Train-validation 보다 높은 정확도 | Train-validation 보다 높은
정확도 | | **특징** | 데이터 set의 분리 비율이
결과에 영향 미침 | 분류의 수에 따라 결과 영향 미침 | 모집단의 분포의 가정 없이
검증 가능 | - 데이터의 양이 충분치 않은 경우, 데이터 모델의 성능 측정의 통계적 신뢰도를 높이기 위해 재 샘플링 기법을 사용하는데, Cross-validation, Bootstrap 이 대표적 방법임
2) 데이터의 수집에 많은 비용 문제로 대부분 데이터의 양이 부족한 현실에서, 재 샘플링 기법을 사용하면 성능 측정의 신뢰도를 높일 수 있음.
3) 대표적인 재 샘플링 기법으로 Cross-Validation, Bootstrap 기법이 있음
### 나. 교차 검증 (Cross Validation)의 정의 - Data Set을 K개의 training Set 또는 부분집합과 나머지 Test Set으로 구분, Training Set을 이용하여 학습하고, 나머지 Test Set으로 성능 측정한 데이터를 얻어,
이에 대한 평균을 구하여 모델 성능을 평가하는 기법 ### 다. Data Set의 구분 |
일부 모형을 조정하여 구축된 모형 중 좋은 모형 선택 | 모델 선택 | ## Ⅱ. 교차 검증 (Cross Validation) 방법 ### 가. Random Subsampling - S를 랜덤하게 k개의 training set과 test set으로 나눔. S_train은 약 70%로 구성하며, 모델 학습용으로 쓰고 나머지 S_cv는 평가용으로 사용. - 각 모델 M_i를 S_train 으로 학습시켜 hypothesis h_i를 구함 - S_cv(h_i)를 적용하였을 때 error(generation error)를 최소화하는 모델선택 - 옵션으로 모델을 선택 후 그 모델에 S_cv도 학습 - 이 방식의 단점은 빼 놓은 30%는 데이터를 학습-평가에 반영하지 않음  - 에러율 : 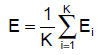  ### 나. k-fold cross validation - Training Set S을 k개의 부분 집합으로 등분, k-1개로 학습하고 나머지 한 개로 테스트. - 각 모델 M_i에 대해 J번째 (j=1,..,k) 집합 S_j를 제외시키고 학습시켜 h_ij를 구하고, S_j를적용하여 generation error 들을 구함 - 모델 M_i의 에러는 각 j번째의 에러들의 평균으로 함. (가장 작은 에러를 갖는 모델 선택) - 그후, 전체 데이터 S로 학습 - 이 방식의 단점은 전형적인 k값은 10이지만, 항상 적정하지는 않고, k값에 따라 계산량이많아짐  - 에러율 : 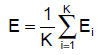  ### 다. Leave-one-out cross validation - k fold cross validation에서, k=N인 경우(N은 샘플 개수) 하나 남기기(Leave-one-out) 또는 잭나이프(Jackknife) 기법 이라 함 - 결국, 데이터 1개씩을 빼가면서 모든 테스트를 하는 방법.  - 에러율 : 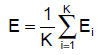  < 1회 >  < N 회 반복 > ## Ⅲ. 검증 방법의 비교 |
집합을 통해서 모델의
정확도를 검증 | 데이터를 k개의 집합으로 나누어
검증한 결과의 평균치로 모델
검증 | 전체 데이터에서 무작위 복원
추출로 훈련집합 생성 하여
검증하는 방법 | | **활용기준** | 데이터가 충분히 많은 경우 | 데이터가 충분하지 않은 경우 |데이터가 충분하지 않은 경우,
모집단 분포 가정 어려운 경우| | **데이터 set** | Train Set, Test Set,
Validation Set | K개의 Set 분류(k-fold)
k-1 : Train set
1 : Test set | N개의 Bootstrap sample | | **정확도** | 에러율 예측의 정확도 다소
**정확도** 낮음 | Train-validation 보다 높은 정확도 | Train-validation 보다 높은
정확도 | | **특징** | 데이터 set의 분리 비율이
결과에 영향 미침 | 분류의 수에 따라 결과 영향 미침 | 모집단의 분포의 가정 없이
검증 가능 | - 데이터의 양이 충분치 않은 경우, 데이터 모델의 성능 측정의 통계적 신뢰도를 높이기 위해 재 샘플링 기법을 사용하는데, Cross-validation, Bootstrap 이 대표적 방법임